Głębia ostrości

  Specyficzny kształt grzybów zawierający elementy obłe i kuliste oraz niewielkie rozmiary wymuszające fotografowanie z bliska sprawiają, że częściej głębia ostrości jest za mała niż za duża. Co to jest głębia ostrości, od czego zależy i jakie stosować środki dla uzyskania dużej głębi ostrości, o tym dyskusja i wnioski poniżej.

  Zjawisko głębi ostrości manifestuje się w ten sposób, że przy nastawieniu obiektywu na określoną odległość przedmioty bliższe i dalsze są nieostre tym bardziej im znajdują się one w większej odległości od punktu ostrości 'w przód' i do tyłu.
  Przyczyna tego zjawiska jest prosta. Promienie świetlne wychodzące od punktów w określonej odległości od obiektywu skupiają się w jednej określonej odległości za obiektywem, im punkt bliżej obiektywu tym jego obraz powstaje dalej za obiektywem, obraz punktów "w nieskończoności" powstaje w odległości równej ogniskowej obiektywu. Powoduje to, że idealny obraz punktów z określonej odległości od obiektywu będzie uzyskany tylko na błonie położonej w określonej odległości za obiektywem. Wszystkie punkty położone za i przed tą odległością będą nieostre (ich obrazem będzie krążek o określonej średnicy, tym większej im większa odległość od idealnej dla danego układu płaszczyzny.
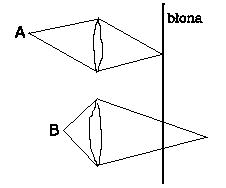Na tym rysunku punkt A ma także punktowy obraz na błonie filmu. Punkt B daje obraz w postaci plamki, ponieważ punkt skupienia znajduje się za błoną. Łatwo domyślić się na podstawie rysunku dlaczego przesłona zmniejsza średnicę plamki rozproszenia a tym samym poprawia ostrość.
  Tak więc idealnie ostry obraz można uzyskać tylko dla obiektów położonych w określonej odległości od błony filmowej. Dla obiektów przestrzennych tego się nie da uzyskać. Na szczęście, dzięki niedoskonałości naszego wzroku, bardzo małe plamki postrzegamy jako punkty. Graniczna rozdzielczość oka to plamki widoczne pod kątem ok. 1'. W praktyce oznacza to, że aby widzieć na odbitce ostre zobrazowanie fotografowanego obiektu - na negatywie małoobrazkowym wielkość krążka rozproszenia powinna wynosić max. 0.03 mm. Taka wartość została też przyjęta dla prezentowanych poniżej obliczeń. Należy zwrócić uwagę, że gdy znacznie powiększa się fragment negatywu - graniczny rozmiar krążka rozproszenia należy przyjąć niższy, przy stosowaniu filmów i błon wielkoformatowych dla uzyskania tej samej wielkości odbitki wystarczy mniejsze powiększenie a co za tym idzie akceptowalny krążek rozproszenia może być większy.
  Jest prosty wzór dzięki któremu można wyliczyć dla danej odległości obiektu do jakiej odległości przed nim i za nim plamka rozproszenia jest mniejsza od granicznej. Wartość liczona wg poniższego wzoru jest używana do tych obliczeń i nosi nazwę odległości hiperfoksalnej:
D = (f * f) / (z * n) , gdzie
f - odległość ogniskowa w mm
z - maksymalna wielkość plamki rozproszenia
n - stopień przesłony
Odległość od przedmiotu do tylnej granicy ostrości:
Tt = (d * (D + f)) / (D - d) , gdzie
d - odległość od obiektywu do fotografowanego obiektu
Odległość od przedmiotu do przedniej granicy ostrości:
Tp = (d * (D + f)) / (D + d)
Na postawie tych wzorów można zauważyć że, głębia ostrości zależy od:
* ogniskowej obiektywu - f,
* przyjętej granicznej wielkości plamki rozproszenia - z,
* stopnia przesłony - n,
* odległości do fotografowanego obiektu - d.
Dyskusji wpływu tych czynników jest poświęcona dalsza część tej analizy.

  Nietrudno zauważyć, że przy fotografowaniu określonym obiektywem mamy największy wpływ na stopień przesłony i w nieco mniejszym stopniu na odległość fotografowania. Używając powyższych wzorów można przy pomocy arkusza kalkulacyjnego dość łatwo zestawić tabelę lub zrobić wykres jak poniżej. Przedstawia on dolną i górną granicę ostrości obiektywu o ogniskowej 58 mm, dla kilku odległości i w zależności od stopnia przesłony.

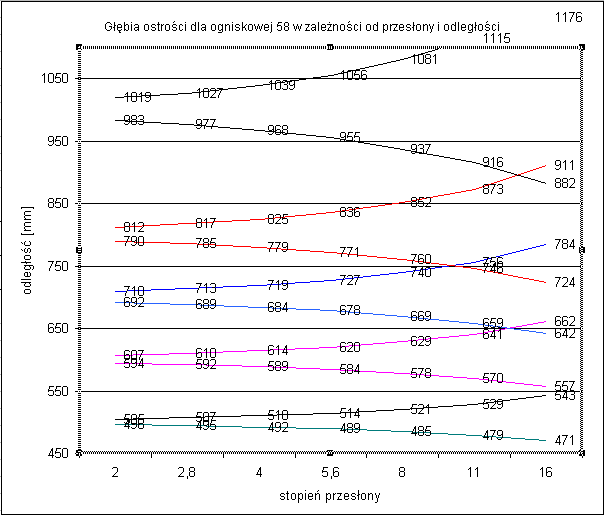
  Jak widać głębia ostrości silnie rośnie wraz ze wzrostem stopnia przesłony i odległości. Czy wystarczy ustawić przesłonę i fotografować z dużej odległości? Aby odpowiedzieć na to pytanie rozważmy jeszcze zagadnienie skali uzyskiwanego obrazu. A to poniżej.

  Przy fotografowaniu rozsądne jest, aby maksymalnie (korzystnie kompozycyjnie) wykorzystać obszar kadru dla przedstawienia fotografowanego obiektu. W przypadku grzybów występuje konieczność odwzorowania w skali od ok. 1:10 do 1:1, częściej bliżej tej pierwszej skali, odpowiada to rozmiarom przedstawianym na kadrze 36 x 24 cm do 3,6 x 2,4 cm. W obiektywach standardowych w odległości minimalnej daje się przeważnie uzyskać skalę odwzorowania nie większą niż 1:9 - 1:5. W przypadku konieczności uzyskania większej skali odwzorowania można zastosować pierścienie przedłużające lub soczewki nasadkowe. Wygodniejszy i lepszej jakości obraz tworzy oczywiście obiektyw makro, który dzięki swojej konstrukcji daje pożądaną skalę odwzorowania bez stosowania sztuczek..
  Jak sobie policzyć skalę odwzorowania? Zależy ona odwrotnie proporcjonalnie od odległości do obiektu i wprost proporcjonalnie od odległości matówki, wg wzoru:
R = v / d, gdzie v to odległość obrazu obiektu od soczewki, a d to odległość od soczewki do obiektu.
  Czyli, aby obraz na błonie był w większej skali należy albo do niego podejść, albo oddalić obiektyw od matówki przy pomocy pierścieni przedłużających lub mieszka.
  Praktycznie, aby policzyć skalę odwzorowania, używa się innego wzoru ponieważ ogniskowa obiektywu f i odległość do obiektu d jest zazwyczaj znana, a odległość od matówki zazwyczaj nie:
R = f / (d - f)
Po przekształceniu tego wzoru można z niego wyliczyć z jakiej odległości należy fotografować, aby uzyskać pożądaną skalę odwzorowania obiektu:
d = (f / R) + f W praktyce dla naprawdę bliskich odległości wzory się na nic nie zdają (liczy się wtedy każdy milimetr, a nie wiemy dokładnie gdzie jest tzw. węzeł optyczny obiektywu). Na szczęście obiektywy makro często mają na pierścieniu ustawiania odległości zaznaczone także odpowiadające im skale odwzorowania.

  Krótko: NIE MA CO NA TO LICZYĆ. Dłużej: Korzystając ze wzorów do obliczenia skali odwzorowania liczyłem odległość z jakiej należy fotografować obiektywem o określonej ogniskowej aby uzyskać określoną skalę odwzorowania. Dla tej odległości liczyłem głębię ostrości. (odległości fotografowania mniejsze od minimalnej dla normalnego obiektywu można uzyskać np. stosując pierścienie wydłużające)
  Analizując pierwszy wykres, który przedstawia wielkość głębi ostrości w zależności od stopnia przesłony i ogniskowej obiektywu, dochodzi się do wniosku, że dla wielkości głębi ostrości ogniskowa obiektywu nie ma praktycznego znaczenia przy skali odwzorowania 1:10 (i jak będzie pokazane później tym bardziej nie ma znaczenia przy większych skalach odwzorowania).

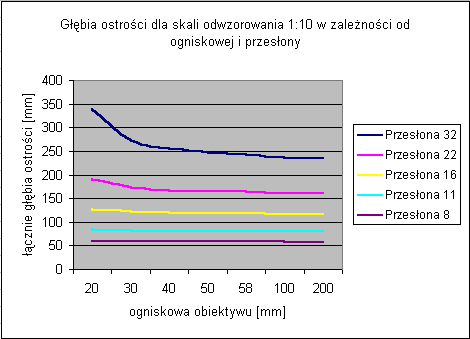
  Jak widać głębia ostrości jest w zauważalnym stopniu lepsza dla obiektywów o krótkiej ogniskowej, ale jedynie dla bardzo dużych stopni przesłony - gdzie i tak głębia ostrości jest dość przyzwoita. Wykres sporządzono dla stosunkowo małej skali odwzorowania 1:10. Na kolejnym wykresie można zauważyć, że wraz ze wzrostem skali ta przewaga krótkoogniskowych obiektywów zanika.

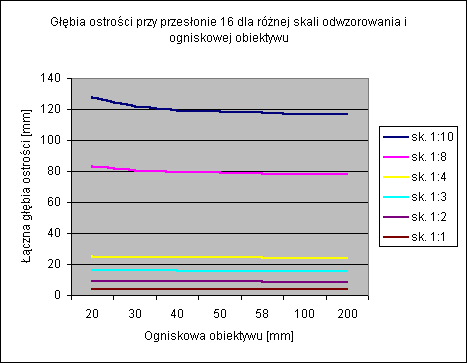
Morały z obydwu wykresów są następujące:
* Nie ma co liczyć na efektywny zysk na głębi przez dobór krótszych ogniskowych.
* Silny zysk na głębi jest możliwy przy zwiększaniu stopnia przesłony.
* Przy dużych skalach odwzorowania co by się nie robiło, to głębia ostrości jest tragicznie mała. Np. przy skali 1:1 dla przesłony 16 wynosi 4 mm a dla przesłony 32 niewiele więcej bo 8 mm i nic się nie da z tym zrobić.

Dlaczego nie można bezkarnie zwiększać przesłony (choć zwykle to nie przeszkadza) możecie przeczytać na stronie o dyfrakcji i rozdzielczości optycznej obrazu.